En los cables de las vías del tren se observa una curva cuya descripción matemática es similar a la del número e.
En el estudio de las ciencias de la naturaleza, como la física o la biología, aparecen con frecuencia ciertos números a los cuales se les da nombre propio debido a su gran importancia en estos campos. Uno de ellos es el número e, conocido como el número del cálculo matemático o la constante de Euler. Pero, ¿por qué es tan importante este número?
Para introducir al número e, primero veamos cómo se define. Nos remontaremos a 1.683, año en el que Jacob Bernoulli, matemático y científico, obtuvo una primera aproximación de esta constante de una forma que nadie se esperaría; resolviendo un problema de finanzas.
Imaginemos que tenemos un euro (tampoco hay que imaginar mucho) y lo queremos depositar en un banco bastante generoso el cual nos ofrece un 100% de interés en un año. Esto significa que al cabo de un año tendremos \(1+1×1=2€\). Bien, hemos doblado la cantidad inicial de dinero que teníamos. Pero ahora surge una pregunta: ¿podríamos conseguir más dinero con otro tipo de interés en un año? ¿Y si tuviéramos un interés del 50% cada 6 meses? En ese caso, al cabo de 6 meses tendríamos \(1+1×0,5=(1+1/2)^1=1,5€\) y 6 meses después (1 año en total)1 acabaríamos con \(1,5+1,5×0,5=(1+1/2)^2=2,25€\). Por tanto, hemos acabado con más dinero que con el 100% de interés del principio. Aunque, ¿podríamos mejorar esto aún más? Imaginemos ahora que el banco nos ofrece un doceavo de interés cada mes. En esta ocasión, y usando un poquito de álgebra, podemos ver que al cabo de un año tendríamos \((1+1/12)^{12}=2,61€\). Como ya estaréis comprobando, a medida que generamos interés de forma más consecutiva acabamos ganando más dinero con el tiempo. A raíz de esto, uno se pregunta qué pasaría si el banco nos ofreciera la fracción correspondiente de interés cada día, o cada segundo, o… cada instante.
Por desgracia, esta ganancia tiene un límite, no crece infinitamente. Consideremos la expresión anterior, pero en lugar de un número pongamos una variable. Tenemos la expresión \((1+1/n)^n\), siendo n un número cualquiera.
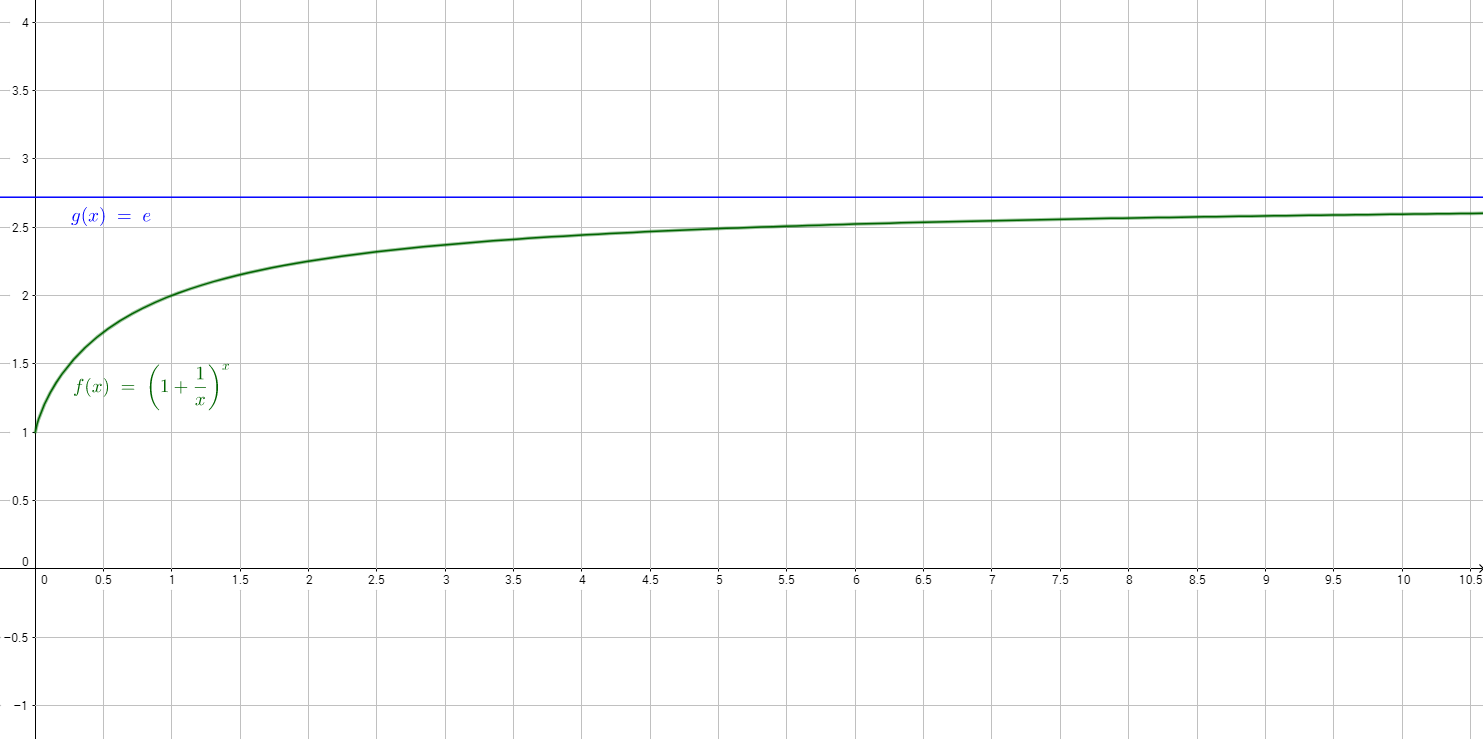
Representación de (1+1/x)^x. Puede verse cómo al aumentar x la función se acerca a e.
Si hacemos crecer mucho n, deberíamos acercarnos a ese valor límite. Bernoulli en el siglo ⅩⅤⅡ trabajó con esta expresión y descubrió que este valor límite estaba entre 2 y 3. Unos años después, Leonhard Euler descubrió el valor de este límite, aunque utilizando un método distinto. Dicho número es 2,71828…2 y es lo que llamamos el número e.
Pero, ¿por qué es este número tan importante? En pocas palabras, e define un lenguaje muy natural para expresar razones de cambio y crecimiento.
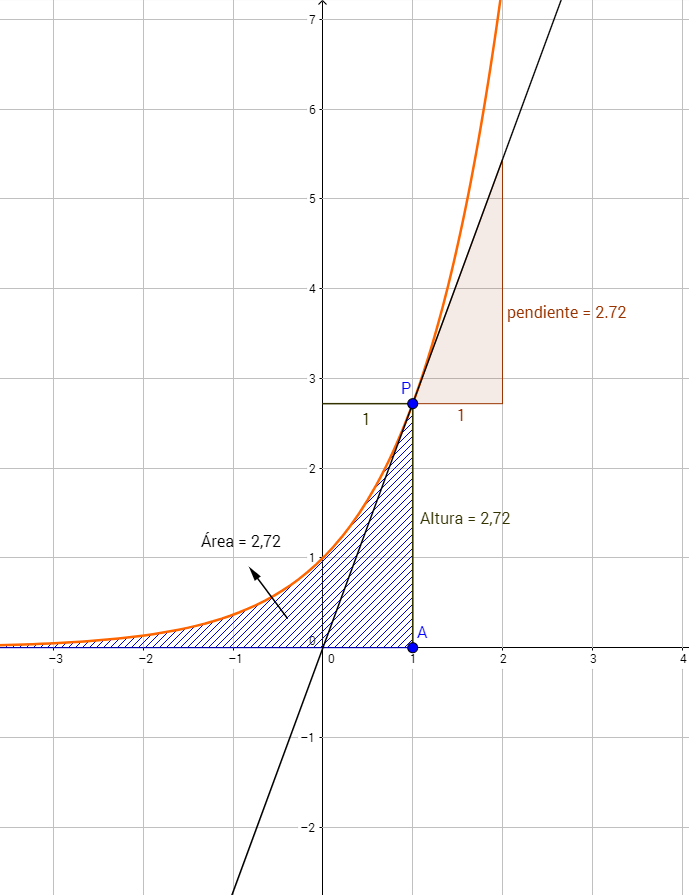
Representación gráfica de la función e^x (en rojo).
La gráfica adjunta nos permite ver dos propiedades que hacen tan especial al número e y a la función exponencial que define.
La primera de ellas es su derivada, o en otras palabras, la pendiente de la recta tangente a la curva en un punto. El concepto de pendiente permite comprender cómo crece el valor de la función a medida que crece x, es decir, responde a la siguiente pregunta: si me muevo un poco a lo largo del eje x, ¿cómo crece \(e^x\)?
Bien, pues en el caso de esta función definida por potencias de x, la respuesta es simple: exactamente ex. Es decir, en x=1, lugar en el que se sitúa el punto P, el valor de la función es e, y la pendiente de la recta tangente al punto P es también e.
Pero esto va aún más lejos. La segunda propiedad es el área bajo la curva de esta función, que cumple exactamente lo mismo que antes. Siguiendo el mismo ejemplo, el área bajo la curva en x=1 sería exactamente igual a e. Es decir, tanto el valor de la función, su derivada y el área bajo la curva son iguales para cada punto de la curva. Y esta es la única función que cumple algo así. ¿Fascinante, no? Esto permite escribir resultados matemáticos y expresar procesos relacionados con crecimiento y cambios de forma muy cómoda, ya que de hacerlo con cualquier otro número aparecerían factores que harían todo bastante más lioso.
Por último, veamos un ejemplo práctico de la constante de Euler en lo que se conoce como el crecimiento exponencial y logístico. Imaginemos que tenemos una muestra de bacterias. Las bacterias se reproducen mediante un proceso llamado fisión o bipartición, mediante el cual una bacteria puede separarse en dos. Si la cantidad de recursos es ilimitada y no hay factores que alteren el proceso, se puede calcular la cantidad de bacterias que habrá en la muestra después de un tiempo determinado mediante la ecuación \(N(t)=N(0)e^{rt}\), donde N(0) es el número de bacterias que había al comienzo, r una constante que indica el ratio de crecimiento de las bacterias y t el tiempo que ha pasado. Este es el crecimiento exponencial, aunque es un modelo algo ideal ya que en la realidad suele haber algún factor que frene el crecimiento o la reproducción. El crecimiento logístico tiene en cuenta este tipo de factores y modela mediante otra ecuación algo más compleja el crecimiento poblacional en estas circunstancias.
Existen muchas más situaciones en las que aparece el número e: en las leyes de enfriamiento de Newton, en el estudio de la descomposición de cadáveres, en la teoría de la probabilidad… Desde luego, es un número sumamente importante por sus propiedades únicas y una herramienta excepcional para los científicos, que en multitud de ocasiones lo encuentran dando forma a las leyes y procesos que rigen la naturaleza.
Notas
| ↑1 | Considerando el caso del 50% de interés, por ejemplo, podemos sacar factor común 1,5 de forma que quede 1,5(1+0,5)=(1+0,5)(1+0,5)=(1+0,5)^2. Esto puede hacerse para cualquier interés que consideremos, y al final, obtendremos la misma expresión cambiando sólo el número del denominador y del exponente. |
|---|---|
| ↑2 | El número e es irracional, es decir, que no puede expresarse como una fracción entre dos números. Como consecuencia tiene infinitas cifras decimales, cosa que demostró Euler mediante una expresión que relacionaba e con una fracción infinita. |